
Search
The Renewable Energy site for Do-It-Yourselfers
Thoughts on the
Ramlow Sand Bed Storage Solar Heating System
| These are some thoughts of mine on the article that Bob Ramlow wrote for
Nov/Dec, 2007 issue of Solar Today on sand bed heat storage. The
article, which is quite interesting, is:
Warm, Radiant Comfort in the Sand, Bob Ramlow ...
As you will see from reading the thoughts below, I'm a bit unclear,
or perhaps even a bit skeptical of some of the stated advantages of the sand
bed. I like the idea of the sand bed and its inherent
simplicity, and would like to be shown that it really does perform well
-- so, if you have more data on this, or think I am off base on some of
the comments please let me know
Gary.... If you have a sand bed storage house and would like
to log its performance, I'd probably be willing to help out.
|
|
This picture from Bob's article shows
the sand bed concept.
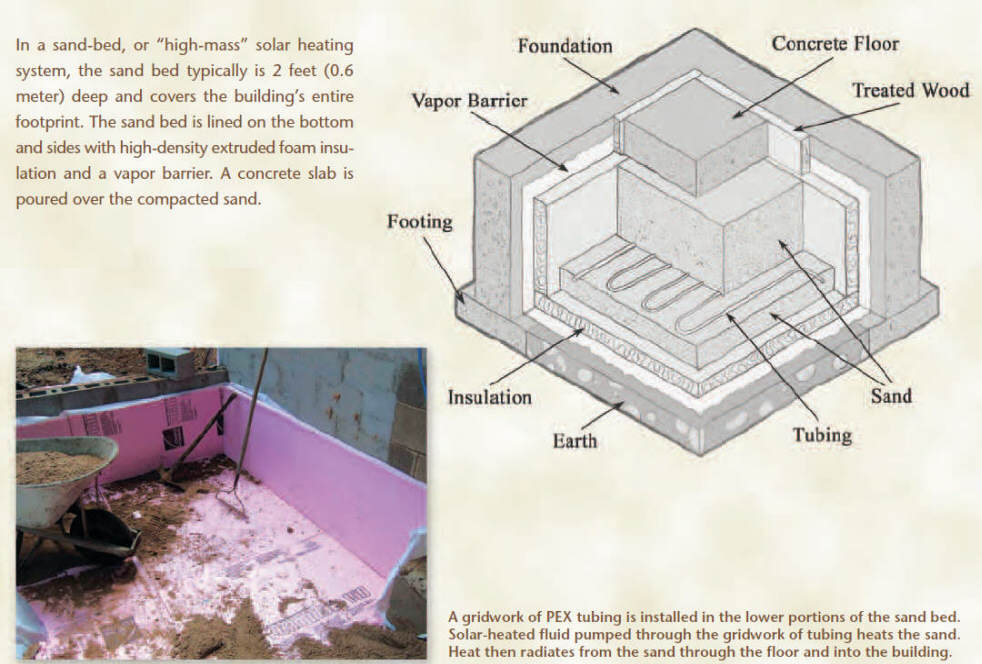
These comments deal with the article,
so you probably want to read the article before reading the comments on it
below.
Basic Collector and Heat Storage
Sizes
Bob says:
"Here in Wisconsin where winters
tend to be long and cold, we
size traditional solar-heating storage tanks at a ratio of approximately
1.25 gallons (4.7 liters) of storage for every 1 square
foot (0.1 square meter) of flat-plate collector or equivalent in evacuated-
tube collectors. Our rule of thumb for sizing collector
arrays is to have 2 square feet (0.2 square meter) of flat plate collector
or equivalent in evacuated tube collectors for every 10
square feet (1 square meter) of the footprint of the building."
If you use a 2000 sqft home as an
example (as Bob does in the article), then for the sand bed house:
Solar collector area by Bob's
ground rule of 2 sf of collector per 10 sf of floor space would be (2000
sqft) (2 sqft / 10 sqft) = 400 sqft of collector area (not a small
collector).
Storage mass by Bob's suggestion
of a 2 ft deep sand bed under the full 2000 sf living area would give (2000
sqft)(2 ft) (100 lb/cf) = 400,000 lbs of sand mass.
The equivalent thermal storage weight of water
storage would be less by the ratio of the specific heats of sand and water.
That is, water stores about 5 times as much heat per lb as sand, so less
water is required.
Equivalent water storage =
(400,000 lbs) (0.2 BTU/lb-F/ 1.0 BTU/lb-F) = 80,000 lbs of water, or
9600 gallons, or 1285 cf
Where 0.2 BTU/lb-F and 1
BTU/lb-F are the specific heats of sand and water
A cube shaped tank to hold
this much water would measure about 11 ft on a side (not counting
insulation thickness).
This assumes that the sand
bed and the water tank are operated over the same temperature range.
It seems likely to me that the water tank could be operated through a
larger temperature band, especially for the fall seasonal storage phase
-- this would reduce the size of the water tank significantly (see
below).
Stored heat in the sand bed when
its fully charged is hard to estimate because no temperature is given for
the fully charged sand bed. If you assume 110F (?) for the charged
sand bed, then the stored heat would be about
Stored heat in sand bed =
(110F - 80F)(400,000 lbs)(0.2 BTU/lb-F) = 2,400,000 BTU
Maybe the 110F maximum
temperature assumed above is too low? Can the house be comfortable
when the storage under the floor is hotter than 110F?
This article:
http://www.radiantsolar.com/pdf/DOEREPORT.pdf would seem to indicate
that even 110F might be too high.
Comments:
- Bob mentions that the 2000
sf example house is well insulated and has some passive solar gain, and
is built to the ground rule above (400 sqft of collector and 4000 cf of
sand bed storage) will have a good fraction of its heat supplied by the
sand bed system.
My first reaction to that is
that 400 sf is quite a bit of collector area, and a well insulated 2000 sf
house with some passive gain and 400sf of active collector is likely to
have a good solar fraction with conventional water tank heat storage.
It would have been helpful to have more analysis to show the detail on
how a house with the same 400 sf of collector and conventional water
heat storage would compare to the same house with sand bed storage.
- Seasonal Storage:
The sand bed is charged in the late summer and early fall, and it will
hold about 2.4 million BTU (see above). How does this compare with
the full heating season demand for such a house?
For a 2000 sqft house in
an 8500 degree day climate, with R60 ceilings, R30 walls, R5
windows, 0.3 air changes per hour, and no heat loss to the floor,
the full season heat demand is about: 52 million BTU.
Internal heat gains might contribute about 18 mllion BTU, so the net
heating need is about 34 million BTU (from this calculator:
http://www.builditsolar.com/References/Calculators/HeatLoss/HeatLoss.htm
)
So, the 2.4 million BTU
stored in the sand bed is about 2.4/34 = 7% of the heating season
demand. I guess this illustrates how hard it is to
store a significant fraction of your full winter heating needs in a
reasonable size heat store -- even for well insulated homes.
- Useful storage temperature
range: It seems to me that if you are directly over the sand bed
storage, and it is tightly thermally coupled to the living area (as it
must be to provide heating), then there has to be a limit to how hot you
can let the sand bed get without overheating the house. This seems like
a key element, but there is no mention (that I saw) of what the maximum
sand bed temperature is. It would have been really helpful
to provide a log of sand bed temperatures at the top bottom and middle
of the sand bed for a full heating season. With data logging
systems only costing a few hundred dollars these days, it seems a shame
not to carefully document the actual performance of these very
interesting sand bed storage homes.
If a large water storage tank
is used instead of the sand bed, the upper temperature limit could be
quite a bit higher because the tank is not directly thermally coupled to
the living area. The 11 ft cube tank mentioned above, which is the
equivalent thermal mass of of the 4000 cf sand bed could actually store
quite a bit more heat than the sand bed going into the winter. For
example, if it were run up to 170F in the late summer/early fall, it
could store about (170F - 80F) (80,000 lbs)(1 BTU/lb-F) = 7.2 million
BTU instead of the 2.4 million for the sand bed -- 3 times the
seasonal heat storage capacity for the same thermal mass heat store.
Again, the maximum
temperature that you can get the sand bed up to and still not overheat
the house seems like a very key issue.
Relative Performance of Sand Bed and
Water Tank Storage Systems
Bob says:
"What Makes Sand Good for
Storage?
The following examples illustrate the differences between
sand-bed storage and water-storage systems. Let us assume that
the model building is a well-insulated, single-story building with
a 2,000-square-foot (186-square-meter) footprint. Using our rule
of thumb to size the collector array (2,000 square feet x 0.2), we
get a 400-square-foot (37-square-meter) array. If using water as a
heat-storage medium, the
water-storage
tank must have a capacity of 400–500
gallons (1.5–1.9 kiloliters). This tank
would weigh between 1.67 tons and
2.08 tons (1.51–1.89 metric tons). If
using a sand bed as a heat-storage medium,
the sand bed must contain 2 cubic
feet (0.06 cubic meter) of sand for every
square foot (0.09 square meter) of the building’s
footprint. A cubic foot of dry, compacted
sand weighs approximately 100 pounds (45.4
kilograms), so for every square foot of the building
footprint the sand bed would have 200 pounds (90.7 kg) of
storage, resulting in 200 tons (181.4 metric tons) of storage for a
2,000-square-foot building. You can see that the sand-bed storage
system has 100 times the weight of the water-storage system.
Heat dissipates quickly in a water tank because water is uniform
and has no spaces between water molecules. Sand, on the other
hand, has spaces between the granules, so heat transfer is much
slower. However, heat can travel in a concentrated path rather
quickly through a sand bed toward cold."
Comments:
- It seems to me that a water
tank storage of only 500 gallons for 400 sqft of collector and a well
insulated 2000 sqft house is too small. If you figure a rough net gain
of 800 BTU/sf of collector on a sunny winter day, the 400 sqft collectors
will be able to send about 320K BTU of heat to storage. The well
insulated house with an average outside temp of 30F will have a heat demand
of about 190K BTU for the day (less with some passive solar gain). So,
even in a single sunny day, a 500 gallon storage tank would be on its way to overheating,
and a series of sunny days would waste a lot of solar heat because the tank
would be too hot to accept it.
It seems to me that the 1.25
gallons of storage per sqft of collector is OK for a typical solar heating
installation where the home heat loss is relatively large (due to average
insulation), and the collector area is relatively smaller relative to the
home floor area, but its to low for a well insulated house with lots of
collector area.
- As mentioned above, the low
heat capacity of sand compared to water and the larger temperature range
that you can operate a water heat storage tank over would allow a much much
smaller than 200 ton capacity tank store the same amount of heat as
the sand bed in the fall. It seems to me that a water tank of around
3000 gallons (a 7.5 ft on a side cube) would provide about the same
seasonal heat storage as the sand bed and would be a not so bad match (if
well insulated) to 400 sqft of collector on a well insulated 2000 sqft home.
The 320K sunny day heat harvest
would warm a 3000 gallon tank about 13F. If this proves to
be a bit
too much tank, perhaps the water tank would want to be partially drained
after the seasonal fall storage has been used? Or, the tank might be
partitioned, or two tanks might be used? But, if the tank is well
insulated, a gain of only 13F on a sunny day might be fine -- it would
increase in temperature slowly over several sunny days, and decline slowly
over cloudy days as the house took heat out of it.
- I don't understand the "heat
dissipates quickly in water" comment. The heating system can draw as
much heat as it needs from the water tank when it needs it. It seems
to me that the heat from the water tank dissipates at whatever rate the
house needs it?
With the sand bed, it seems to me
that since the thermal store (the sand) is directly coupled to the living
area, the heat transfer rate to the living area will depend largely on
the temperature difference between the living area and the heat store.
When the heat store is hot, there will be a higher rate of heat transfer
than when the store is cooler. This seems like a
disadvantage over the water tank system in that what you really want is a
heat transfer rate to the living area that depends on how cold it is outside
-- it seems to me that the water tank storage with an appropriate control
system gives you this, while the sand bed does not? Maybe I'm missing
something?
Heat Loss From Storage
One item that is not mentioned in the
article is the heat loss to the outside from the storage tank.
The sand bed store has a heat loss
area to the outside of about 2400 sqft. It looks like the pictures
in the article show 2 inch XPS insulation being used to insulate it, for an R
value of R10. Its not straight forward to estimate the heat loss from the
sand bed storage over the course of the heating season because the soil
temperature is not easy to estimate and will be changing, and the sand bed
temperature also changes. But, if you use the soil temps that were
measured in
this paper, it looks like 55F for under the sand bed, and 34 F for the sides
of the sand bed might be in the ball park. And, assuming a winter long
average sand bed temperature of 80F(?), the heat loss would roughly be:
Sand Bed Heat Loss = (80F -
55F)(2000 sf) / (R10) + (80F - 34F)(400 sf) / (R10) = 5000 BTU/hr + 1840
BTU/hr = 6840 BTU/hr or 164 K BTU/day
This seems quite high -- its not
a whole lot less than the heat loss for the whole house.
I have to wonder how much of an
issue the heat loss from the sand bed storage to the surrounding earth is.
It seems like a very large heat transfer area between something you want to
keep its warmth and the cold dirt, and only R10 between them?
A water storage tank that stores an
about equivalent amount of seasonal heat by fall would be around an 8 ft on a
side cube, or 380 sf of heat loss area -- only 15% of the heat loss area of the
sand bed.. Much thicker insulation could be used on the water tank for the same cost. The
tank could also be positioned so that some of the heat loss is beneficial (eg in
the basement or conditioned crawl space).
On the other hand, the average water tank temperature will probably run higher than the
average sand bed temperature, so this would increase water tank losses. If
one assumes a tank positioned in a conditioned crawl space or basement that
averages 55F, and an average full winter tank temperature of 110F, and 6 inches
of polyiso insulation, then the heat loss would be:
Water Tank Heat Loss = (110F -
55F)(380 sf) / (R39) = 540 BTU/hr or 12,900 BTU/day
This is less than a tenth of the
rough estimate of sand
bed loss, and some of this loss would be recovered because the tank is located
in a semi-conditioned area.
Again, these are very rough
estimates, but they do seem to me to indicate that heat loss from storage is a
more difficult proposition with the sand bed storage than for a water tank
storage system?
Gary December 30, 2010

