| N. Pine, Pine Associates Ltd., 821 Collegeville Rd., | P. Bashus, Physics Dept., Ursinus College, |
| Collegeville, PA 19426, USA | Collegeville, PA 19426, USA |
| (484) 973-6701 nick_pine@verizon.net | (610) 409-3000 pbashus@acad.ursinus.edu |
Note: 2014 Update from Nick Pine at end of article.
Nick Pine's blog...
A "solar closet" is an insulated box filled with sealed containers of water, with a solar air heater attached to one insulated side. In a simplified solar space- and water-heating technique, a low-thermal-mass isolated sunspace heats a house on an average winter day, with an average amount of sun. A higher-temperature, compact, high-thermal-mass sauna behind the sunspace provides domestic hot water and space heat for the house during cloudy weather.
Passive, solar, space, water, house, heating.
Many solar houses are expensive and low-performing. Active systems can perform well, but they tend to be expensive and complicated. "Trombe walls," invented in 1881 (US Patent No. 246,626), by Edward Morse of Salem, Massachusetts, are still being used in today's passive solar houses. However, because they are so poorly insulated, Trombe walls perform poorly on cloudy days... A person might well build a typical passive solar house, and end up with a house that costs more than a neighbor's, while only using 30% less oil for heating. Some passive solar houses take 20 years to pay for their passive features, versus non-solar houses. A direct-gain passive solar house typically has a very large uninsulated window in a living area, with a masonry floor in front of that, to store solar heat. This works well in sunny climates, with few cloudy days in a row.
However, cloudy-day performance becomes more important as we approach 90-100% solar heating. Sunny-day heating is taken for granted; domestic water heating becomes more important. With the end of solar tax credits, dollars saved per dollar invested and annual backup heating fuel bills become more important. Solar houses now need to stand on their own economic feet, as do superinsulated houses. They can be combined…
Typical solar houses have limitations: masonry floors and walls are not good "heat batteries." Water is less expensive than masonry, and stores about three times more heat by volume, with a lower thermal resistance. We cannot cover masonry floors with rugs on a sunny day. Perhaps they should be covered at night... A direct gain house has an optimal solar glazing/heat load ratio: too little glazing gives too little solar gain, and too much glazing allows too much cloudy-day heat loss. A direct gain house gets exponentially colder with each cloudy day, barring a backup heating system. A higher temperature, more compact, better-insulated heat store that is maintained at a temperature of, say 54oC vs. 20oC, will have a longer discharge lifetime and can provide controllable heat for a house during longer strings of cloudy days. In a direct gain house, we have to live inside the heat store, so we cannot charge it up to a high temperature during sunny weather.
Solar closets solve the problem above, as well as the "optimal solar glazing area" dilemma. A simple solar closet is an insulated cube, with some sealed containers of water inside and a passive solar air heater attached to one insulated side. How much water and how much insulation? A cube with about half water and half insulation by volume will maximize its natural (RC) time constant, prolonging the discharge lifetime of this heat battery.
We arrived at this conclusion by differentiating the formula for the RC time constant. However, the use of calculus seems overdone in solar heating. Many practical solar heating systems can be designed with arithmetic and, at most, algebra or computer tools. Voltaire (1764) said, "The best is the enemy of the good." He meant that it is better to do calculations on the back of an envelope and go build something than to spend one's life on earth designing better and better systems without ever building one. This includes the pursuit of better materials as well as mathematical and physical models. The energy crisis is not over yet, and very few houses are 100% solar heated. Let's take a step backwards in our sophistication and let builders and architects design simple, high-performance, passive solar houses using simple assumptions and arithmetic, just as they do simple beam design calculations.
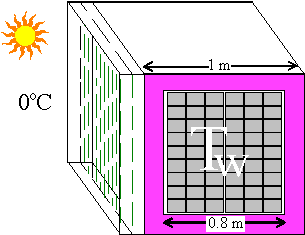
Consider a 1 m cubical solar closet (Fig. 1A) sitting outdoors on an average 0oC December day near Philadelphia, Pennsylvania, USA. The south wall of the closet, i.e., the solar air heater, receives about 3 kWh/m2/day of solar heat, i.e. Ein = 3 kWh/day, more if there is snow on the ground or a white surface or a shallow frozen reflecting pool in front...
Say the closet has 10 cm of insulation with a metric R-value of 4 m2 oC/W, and it contains an 80 cm cube of water in 1 or 2 liter plastic soda bottles or rectangular 3 liter olive oil cans, with some spaces for warm air to flow around the cans. The cans have about 14 times the glazed area. During an average 6 hour December day, the closet loses heat through the R0.1 single-pane glazing of the air heater, and during all other times it is well-insulated, and the air and water temperatures inside the closet and the air heater are all the same, Tw, then the heat flow out of the closet on an average day is
Eout = 6 hr (Tw-0) 1 m2/R0.1 south (equatorial) wall, day
+18 hr (Tw-0) 1 m2/R4 south wall, night
+24 hr (Tw-0) 5 m2/R4 other walls
= (Tw-0)(60 + 4.5 + 30) = (Tw-0) 94.5, (1)
so if Ein = Eout, then Tw = 0 + 3k/94.5 = 31.7oC. (2)
Note that the solar closet is acting like a stagnated solar collector, with some thermal mass inside just keeping itself warm, not a whole attached house. This is a "naturally-trickle-charged heat battery," with a solar collection efficiency of 0. How long will it take to discharge to 20oC inside?
When the sun is not shining, the cube has a thermal resistance of about R4/6 m2, and a capacitance of about 0.5 m3 x 1 kWh/m3C, so its time constant is RC = 500 hours or about 20 days. Taking logarithms, we find
the time t in the equation 20oC = 0oC + (31.7 - 0) exp(-t/20) (3)
is 9.6 days. Not bad for a solar house, but this is more like
an aquarium...
| A)
 | B)
 |
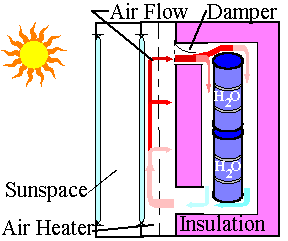
Fig. 1 - A 1 meter solar closet (A) and a larger system (B) showing airflow.
An 2 m cube containing 18 - 200 liter drums full of water with a 9:1 drum/glazing area ratio (bigger closets can use bigger containers), and 20 cm of insulation would work better, with a time to cool to 20oC of 33 days. A 4 m solar closet with R16 insulation would take 5 months (156 days) to cool to 20oC, at a constant 0oC outside with no sun, using these simple assumptions. As a rule of thumb, the time constant in weeks of a solar closet is roughly its dimension in meters, squared.
The passive air heater absorber above might be a thin, black-painted sheet of metal with some holes in it, as in the Conserval air heater, with cooler air moving south from the lower part of the closet (Fig. 1B), up through an airspace between the glazing and the absorber, sideways from south to north, through the absorber plate, into an airspace behind the absorber, and back into the top of the closet via a hole in the insulated south wall. As an alternative the absorber might be black window screen or 80%-absorbing, black, porous, greenhouse shadecloth, costing about $2/m2, perhaps behind some green shadecloth, for aesthetics. The glazing might be 0.05 cm thick single-layer, clear, flat, non-fibrous, semi-rigid polycarbonate plastic, costing about $10/m2. The top of the air heater needs a passive plastic film air damper to prevent reverse airflow at night. We might control airflow by using an inexpensive automatic damper (e.g., the $11 FV-1B automatic foundation vent made by Leslie-Locke of Atlanta, GA) with a bimetallic spring to open some louvers to let air flow when the air is above an adjustable soft threshold temperature, as in a spacecraft cooler. Two opposed springs might make a differential thermostat. Another way to prevent reverse airflow at night is to put the containers of water above the air heater, as in igloos, or the attic warmstores of Norman Saunders, P. E.
As an alternative, a small fan with a backdraft damper would move air faster, raising heat flow rates and lowering air film thermal resistances for the absorber and water container walls, thus increasing solar collection efficiency. Figure 1 of ASHRAE (1993) shows thermal conductivity U (=1/R) of surfaces increasing linearly with air velocity. However, solar collection efficiency is not important here, since almost all the heat losses from the solar closet end up in the house. A fan would allow shrinking duct widths required for natural airflow, which Baer (1979) estimates as 1/15 of the collector area.
How do we turn a solar closet into a house? Building the house around the solar closet allows the closet to have less insulation or operate at a higher temperature, since most of the closet walls can be inside the house, exposed to 20oC air versus 0oC air, with no wind. The air heater wall should be inside a sunspace, to keep it warmer during the day, when losses are greatest.
A low-thermal-mass sunspace can heat the house on an average winter day. Transparent "solar siding" with an air gap and insulation behind it can make a very thin sunspace. Houses need siding anyway, and corrugated clear polycarbonate plastic sheets cost about $10/m2 and last many years. We might use a commercial plastic film greenhouse for a sunspace, or a steep equatorial-facing transparent roof over an insulated ceiling, blowing down warm air to the house from this low-thermal-mass solar attic with a fan.
Size the sunspace to keep the house at 20oC on an winter average day. The solar closet would merely keep itself warm, leaking most of its "waste heat" to the house, not to the outdoors, lying in wait, lurking, ready to provide heat for the house at night, or during a string of cloudy days. It could be in the airpath of a hot air heating system, with a bypass damper that allows heat to flow out of the closet as needed, or a motorized air damper near the top of the closet, controlled by a thermostat or a setback thermostat could open the damper from the closet to the house. Reversing the spring in the foundation vent mentioned above would allow its louvers to open to let warm air into the house as the house cools. An open attic warmstore, e.g., a vaulted stone ceiling or concrete dome with foam on the outside might use a ceiling fan controlled by a thermostat to blow warm air down into the house as needed.
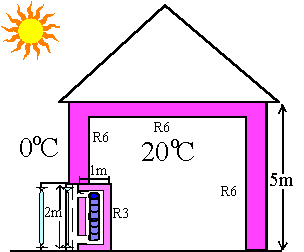
Suppose our new passive solar house is in Philadelphia, where the average temperature is about 0oC and about 3 kWh/m2/day falls on the south wall of a house on an average day in December, with some sun. NREL (Marion and Wilcox, 1994) give this data for many U.S. locations. NREL/NOAA also supply hourly solar weather data on CD-ROM (orders@ncdc.noaa.gov). Suppose our well insulated house is 10 m x 10 m square, and two stories tall (Fig. 2), with about 300 m2 of walls and ceiling, with an average R-value of 6 and a heat capacity equivalent to 10 kg of water/m2, with no air infiltration or internal heat generation.
| A)
 | B)
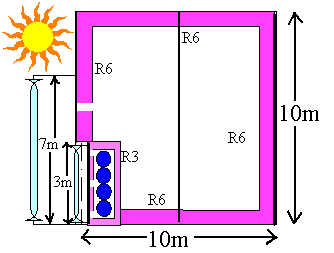 |
Fig. 2 - Solar closet house, side (A) and plan views (B)
Using "Ohm's law for heatflow," 24 kWh/day will keep the house 20oC inside when it's 0oC outside, about the same as a gallon of oil, burned inefficiently. A square meter of glazing attached to the low-thermal-mass wall of this house would gain about 3 kWh and lose about 6 hr (20oC - 0oC)/R0.1 = 1.2 kWh, for a net gain of 1.8 kWh. Our house would thus need 24 kWh/1.8 kWh/m2 = 13.3 m2 (~2 m x 7 m) of sunspace glazing to keep it warm on an average December day, with some sun. Sun-warmed air would flow into the house from the sunspace during the day through holes at the top and the bottom, with dampers, and this low-thermal-mass sunspace would get icy cold at night, unlike a Trombe wall. The house would stay reasonably warm at night with the thermal mass of its walls and floors, i.e.,
20oC - 18 hr x 1 kW/ (300 x 10) Wh/oC = 14oC. (4)
If the sunspace were a greenhouse, it might have an automatic damper to allow warm air to flow from the house as needed to keep the plants just above freezing.
To keep the house warm for say, 5 days without sun, we need to store 120 kWh. A 200-liter drum of 54oC water stores about (54oC - 24oC) 200 liters = 6 kWh of usable space heating energy, so the closet needs 120 kWh / 6kWh = 20 drums full of water inside. These could be stacked up vertically in a rectangular array 2 m high x 3 m wide x 1 m deep, with R3 insulation all round. Let's check the drum water temperature: after a long string of average days in December, with an average amount of sun, the steady-state water temperature Tw would be such that
Ein = 2 m x 3 m x 3 kWh/m2 /day = 18 kWh / day, and (5)
Eout = 6 hr (Tw - 20) 6 m2/R0.1 south wall, day
+18 hr (Tw - 0) 6 m2/R3 south wall, night
+24 hr (Tw - 20) 18 m2/R3 other walls
= (360 + 36 + 144) Tw - 7.2k - 2.88k. (6)
So if Ein = Eout then Tw = 28.08 kWh / 540 = 52.0oC. (7)
| A)
 | B)
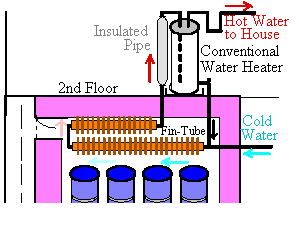 |
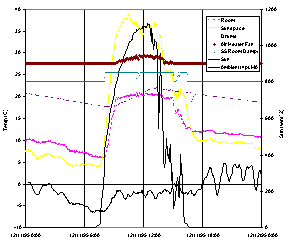
Fig. 3 - Preliminary experimental data (A); Fin tube water heating with a solar closet (B)
We have built and tested a small outdoor structure. Figure 3A shows some results, using a sunspace-to-room motorized damper for daytime temperature control. The numbers and annotations are readable in the full-size version of Figure 3A (115 KB).
A conventional electric water heater might work well on the floor above, with a larger solar closet, in a warm water connection loop with about 5 m of fin-tube mounted near the closet ceiling. Natural water convection flow could provide sufficient hot water for a typical home, using a standard water heater. The tank might need larger input and drain fittings to make this work well. Assuming convective water flow is not a limiting factor, how much air-water heat exchange area is needed inside a solar closet for water heating? One meter of copper fin-tube baseboard pipe provides about 600 W to a 20oC room, if the moving water inside is at 80oC. So each meter of fin-tube passes approximately 600/(80-20) or 10 W/oC water-air temperature difference. How would our water heater work using fin-tube pipe?
Suppose the closet air temperature is 54oC and the hot water consumption of the house consists of 5 showers a day, each lasting 10 minutes, at 10 liters/min using 44oC water heated from 14oC. Each shower uses 100 liters of hot water. How much fin-tube would we need to support this daily average heat transfer rate? If the fin-tube is X meters long, then
RC = 500 liters x 1 Wh/literoC / 10X W/oC = 50/X hr, and (8)
44 = 54 - (54 - 14) exp(-24 hr x X/50), so (9)
X = 2.9 m.
This fin-tube "solar collector" can be small, because it works 24 hours a day. Figure 3B shows a system for heating water with a fin-tube air-water heat exchanger near the ceiling and a conventional insulated water heater on the floor above. If hot water circulates through the heater tank from the closet, the heating element should seldom turn on.
Given a room that is 54oC for 24 hours a day, one might well add some floorspace to make a sauna, perhaps with a small woodstove, or make a place to dry clothes, with a closet-sunspace damper controlled by a humidistat and a differential thermostat to let sunspace air into the solar closet, if it is warmer.
The water in the solar closet might be wastewater in concrete
septic tanks or EPDM-rubber-lined plywood tanks with lids. Sewage
treatment rates double every time the temperature increases 10oC.
Metcalf and Eddy (1991) describe thermophilic anaerobic digestion
as occurring at temperatures of 49oC to 57oC,
where thermophilic bacteria work much faster than mesophilic bacteria.
U.S. Patent No. 3,933,628 describes an anaerobic digester for
a 100,000 cow feedlot, using EPDM-rubber-lined trenches to produce
200k m3 of methane per day. The inventor suggests a
temperature range of 32oC to 46oC, but to
avoid temperature shock, the process should have a daily temperature
variation of at most +/- 1oC. A 3m cube of water cooling
1oC loses ~30kWh, comparable with the daily house heating
load of our example.
ASHRAE (1993) In: 1993 ASHRAE Handbook of Fundamentals, I-P Edition (Robert A. Parsons, ed.) p. 22.1. Approximate relationship: U = 1.5 + v/5, for smooth surfaces, and U = 2 + v/2 for rougher surfaces, e.g. stucco, where U is in Btu/hrft2oF and v is in miles per hour.
Baer, Steve (1979) In: Sunspots, pp. 62-66. Cloudburst Press, Seattle.
Marion, William & Stephen Wilcox (1994) Solar Radiation Data Manual for Flat-Plate and Concentrating Collectors. National Renewable Energy Laboratory, Golden, Colorado.
Metcalf & Eddy, Inc. (1991) In: Wastewater Engineering (George Tchobanoglous, et al., ed.) p. 834. McGraw-Hill Publishing Company, Sydney.
Voltaire (1764) In: Dictionnaire Philosophique, "Le mieux est l'ennemi du bien" (art dramatique.)
The authors wish to thank Steve Baer, Lynn Baumeister, Debbie Malone, Howard Reichmuth, P.E., Norman Saunders, P.E., Carol Warrington, and Malcolm Wells for their encouragement. William Beckman, Ph.D., William Rosenthal, Ph.D., and William Shurcliff, Ph.D., have also been helpful.
March 2, 2014: Update from Nick Pine:
We wrote that paper for the 1996 4th World Renewable Energy Conference in Denver. A few thoughts sinc then:
Solar closets are slow trickle-charged animals, compared to agile sunspaces with lots of daily heat transfer. I'd like to discuss the efficiency of combining lots of daily low-temp solar collection with a little high-temp long-term solar collection. Solar closets are like the solar attics of Norman Saunders, with lots of smallish water containers getting heat from solar-warmed air. Lawn boilers and car radiators may be more practical. I'm still distressed at seeing people build direct gain houses with huge amounts of room-temp thermal mass.
Nick
Nick's blog -- Ask the Renewable Engineer...